从统计学的角度来说，这个问题属于两个总体比例之差的显著性检验。同样的，后面还可能涉及两个总体均值之差的显著性检验。这两个显著性检验也就构成了互联网业内适用面最广的A/B测试的理论基础。
公式如下：

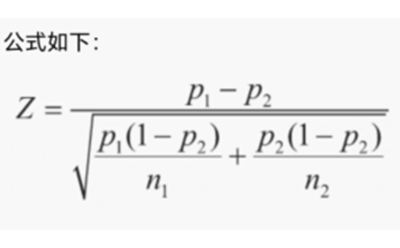
代入1.2.1例子的具体数值，得出：
p1=6.4%，n1=10000；p2=5.6%，n2=10000；
计算得z=2.38，或者把p1和p2换个位置，就得到z=-2.38。
　　此时的z值是大于1.96和小于-1.96的，属于那剩下的5%的情况。所以可以做出判断，原假设是错误的，相反的假设是正确的，即“试验版本_1和原始版本的　　转化率是有显著差异的”，换句话说，A/B测试是成功的。
　　再深究一点，此时的p值是小于0.05的，具体是多少？
　　这里需要用到z值的分布表，大家可以在任何一本统计学教材的附录或者百度上找到它。
　　还记得刚才计算的z值吗？对，2.38，在图2-7的分布表中，我已经把它圈出来了，对应的概率是1-0.9913=0.0087。

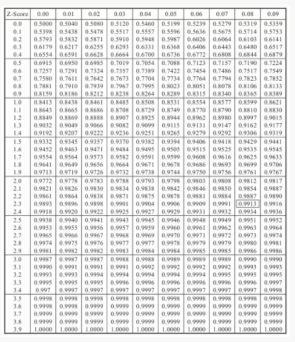
图2-7　正态分布z值分布表
　　注意：我们之前讨论的一直是双边检验，就是说试验版本可能比原始版本更好，或者更差。
　　左边0.025加上右边的0.025，才构成剩下的5%。
　　在广告优化中也是如此，我们的优化策略可能使效果更好，也可能更差。
　　所以，刚才的0.0087还需要乘以2，得到0.174，这才是真正的p值。
　　这里给大家分享一个在线的小工具，可以非常简单地计算出两个总体比例的显著性差异，如图2-8所示：https://vwo.com/ab-split-test-significance-calculator/。

图2-8　A/B测试小工具-1
　　第一列是Control，即控制组（原始版本），在广告优数据分析中用于对比参照的样本；
　　第二列是Variation，即试验组（试验版本），是优化操作后所得到的数据；
　　第一行Number of Visitors，是指流量数；
　　第二行Number of Conversions，是指转化数。
　　接下来，我们用数据演示一下，如图2-9所示。

　　在Control和Variation两列，输入对应的数据，控制组是10000和560，即为流量是10000，转化量为560，转化率为5.6%；试验组是10000和640，即为流量是10000，转化量为640，转化率为6.4%；
　　下面的p值显示为0.009，是不是很接近我们刚才计算的0.0087；Significace显示Yes，说明是有显著性差异的。
　　这个工具还可以帮助我们找到临界值，比如转化率从5.6%提升到6.4%是显著优化的，但其实应该不用到6.4%就可以满足显著性差异，这个临界值是多少呢？
　　我们把Variation列的Number of Conversions不断调小，最终找到临界值是6.15%，如图2-10所示。换句话说，只要我们的优化操作能在同样10000的流量前提下，将转化率提升至超过6.15%，就可判定试验组是显著优于控制组的，即优化是显著有效的。
　　两个总体比例之差的显著性检验的适用范围很广，凡是需要对比优化操作前后的广告效果时，这种显著性检验能很方便快捷地得到结论。同时，要注意这种方法论以及工具的局限性——只能对两个总体比例做检验。包括但不限于：点击率、激活率、注册率等转化率的数据指标，不包括展现量、点击量、注册量、线索量等流量的数据指标。

图2-10　A/B测试小工具-3